If one can view transformers as Markov chains, then limiting results for Markov chains apply to transformers.
Cosma noted for example that “[t]here are finite-state probabilistic languages which cannot be exactly represented by finite-order Markov chains.“. There are also arguments that finite-state, finite-order Markov processes cannot model human language in principle (Debowski).
For Cosma and others (Karpathy, Li, Bertsekas) it is obvious that transformers are Markov models. For me not so much (and there are glaringly wrong takes on the issue too! – see for example here). To convince myself I had to look into the details. So I guess what follows will be mostly of interest to fellow philosophers who are struggling through the thicket of ML tutorials and formal treatments of stochastic processes, somehow trying find the connections.
I’ll try to do this as informal and elementary as possible. Before I can say what a Markov process is, one should quickly remind oneself of what random variables are. For our purposes its enough to remember that they are functions which map events to states: ![]() . As it will turn out that our states are finite and events are countable, we don’t need to worry about any measure theoretical technicalities.
. As it will turn out that our states are finite and events are countable, we don’t need to worry about any measure theoretical technicalities.
A Markov process is a collection of indexed random variables ![]() with the added requirement that the probability of any state
with the added requirement that the probability of any state ![]() depends only on the probability of the preceding state
depends only on the probability of the preceding state ![]() , the so called Markov property. This is also a first order Markov process. The definition can easily be extended to second order and so on. A
, the so called Markov property. This is also a first order Markov process. The definition can easily be extended to second order and so on. A ![]() -th order Markov process is thus a collection of indexed random variables
-th order Markov process is thus a collection of indexed random variables ![]() with the added requirement that the probability of any state
with the added requirement that the probability of any state ![]() depends only on the probability of the preceding k-states
depends only on the probability of the preceding k-states ![]() ,
, ![]() ,…,
,…, ![]() .
.
If the set ![]() of states is finite the Markov process is called finite state Markov process. If the Markov property has the same conditional probabilities for all time steps
of states is finite the Markov process is called finite state Markov process. If the Markov property has the same conditional probabilities for all time steps ![]() , the Markov process is called time-homogeneous.
, the Markov process is called time-homogeneous.
To show that a transformer (i.e. GPT) is a finite k-th order Markov process one needs:
- to identify the sets
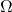 (events),
(events), 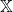 (States) and the random variables
(States) and the random variables 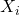
- show that 𝕏 is finite (finite state Markov process)
- show that the transformer forward pass has the k-th order Markov property.
- perhaps show that the Markov process is time homogeneous
I will treat Algorithm 10 in Phuong, Hutter as a reference implementation for a transformer model (i.e. GPT). Inputs are hyperparameters, parameters ![]() and string
and string ![]() . The output is a matrix where the t-th column (vector) gives an estimate of the probability of the next token
. The output is a matrix where the t-th column (vector) gives an estimate of the probability of the next token ![]() . Karpathy has a very nice example of nano-gpt as Markov chain, which helps illustrate some of the more opaque parts in Phuong and Hutter’s pseudocode.
. Karpathy has a very nice example of nano-gpt as Markov chain, which helps illustrate some of the more opaque parts in Phuong and Hutter’s pseudocode.
- (Events)
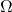 are all possible sequences constructed from the tokens. We use this construction of the event set, because it is natural to run GPT with the outputs of previous GPT passes as input.
are all possible sequences constructed from the tokens. We use this construction of the event set, because it is natural to run GPT with the outputs of previous GPT passes as input. - (States)
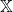 are all possible sequences of tokens up to context length
are all possible sequences of tokens up to context length 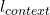 . This means that
. This means that 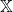 is finite.
is finite. - To reiterate,
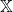 is finite because strings with a length bigger than the context length get cropped (if you don’t believe me see for yourself in line 313 of model.py: “if the sequence context is growing too long we must crop it at block_size“). If the initial segment of strings is identical up to the context length they are indistinguishable and GPT ends up in the same state for them.
is finite because strings with a length bigger than the context length get cropped (if you don’t believe me see for yourself in line 313 of model.py: “if the sequence context is growing too long we must crop it at block_size“). If the initial segment of strings is identical up to the context length they are indistinguishable and GPT ends up in the same state for them. - (Random variables)
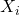 are successive forward passes of GPT. I will write the
are successive forward passes of GPT. I will write the 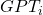 as corresponding random variable at pass
as corresponding random variable at pass 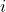 . This is not 100% correct as GPT defined by Phuong and Hutter has strings as inputs and next token probabilities as output. But in the terminology of Markov processes one should really focus on the internal state of one GPT pass. Note that this internal state is indexed by the complete string of GPT’s next token prediction.
. This is not 100% correct as GPT defined by Phuong and Hutter has strings as inputs and next token probabilities as output. But in the terminology of Markov processes one should really focus on the internal state of one GPT pass. Note that this internal state is indexed by the complete string of GPT’s next token prediction.
Also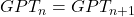 for all
for all 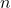 , because we are using the same GPT in every pass. This means the process is time-homogeneous.
, because we are using the same GPT in every pass. This means the process is time-homogeneous. - Markov property. In any forward pass of GPT all (hyper-)parameters
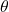 are fixed.
are fixed. 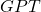 can thus only be a function of strings
can thus only be a function of strings 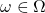 . As already mentioned input strings longer than
. As already mentioned input strings longer than 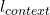 get cropped. The same GPT is used in every time step (time-homogeneousness), so the stochastic process simply is
get cropped. The same GPT is used in every time step (time-homogeneousness), so the stochastic process simply is 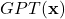 ,
, 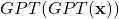 , … ,
, … ,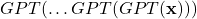 , for the desired sampling time (i.e. the desired length of the continuation of the input string). I will denote the state (or string) after
, for the desired sampling time (i.e. the desired length of the continuation of the input string). I will denote the state (or string) after 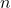 GPT passes as
GPT passes as 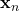 . Because only this string
. Because only this string 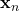 is used to initialize the next pass, the probability of being in state
is used to initialize the next pass, the probability of being in state 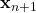 can only depend on
can only depend on 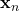 . This means GPT forward passes have the (first-order) Markov property.
. This means GPT forward passes have the (first-order) Markov property. - k-th oder Markov property? The order of the Markov property depends on the construction of the state space
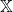 . We identified states with possible strings up to context length. I think this is the most natural way of constructing the state space, but other ways are conceivable. For example one could use tokens (the vocabulary) as states. Then the
. We identified states with possible strings up to context length. I think this is the most natural way of constructing the state space, but other ways are conceivable. For example one could use tokens (the vocabulary) as states. Then the 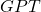 random variable would map from input strings to the next token. And we would need
random variable would map from input strings to the next token. And we would need 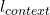 different
different 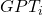 variables to account for all distinguishable input strings. The probability of being in state
variables to account for all distinguishable input strings. The probability of being in state 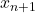 (this is now a token, not a string!) depends then on all previous
(this is now a token, not a string!) depends then on all previous 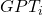 variables with
variables with  . Thus we have a
. Thus we have a 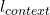 -order finite state Markov process.
-order finite state Markov process.
So Cosma and the others were right. Transformers (at least GPTs as defined by Phuong and Hutter) are finite state Markov processes. The finiteness of the states as opposed to the order is, I think, the important part for thinking about their limitations. Interestingly in his book on language modelling Debowski seems to think that artificial neural networks are not limited by being finite state Markov processes: “[… ] finite-state processes had been an important tool in computational linguistics until they were replaced by artificial neural networks, which proved to be more accurate.” (p.73) This seems off, as we have just convinced ourselves that GPT (a deep neural network) is a finite state Markov process…
If any relevant limitations follow for transformers because they are finite state Markov processes is perhaps a topic for another post.